Convolution & Correlation

신호처리 수업이나 서적

Convolution은 Linear Time Invariant System상에서 이전 값과 현재값을 연산하기 위한 연산

 

Deep learning & imagine analysis

이미지내에서 feature를 출력하기 위한 용도로 연산

 

Convolution에는 확률, 통계, 컴퓨터 비전, 자연어 처리, 이미지 및 신호 처리, 엔지니어링 및 미분 방정식이 포함 된 응용 프로그램이 있습니다.

 컨볼 루션의 일반화는 수치 분석 및 수치 선형 대수, 그리고 신호 처리에서 유한 임펄스 응답 필터의 설계 및 구현에 응용됩니다. 컨벌루션 연산의 역을 계산하는 것을 디컨 볼 루션이라고합니다.

[원문]

Convolution has applications that include probability, statistics, computer vision, natural language processing, image and signal processing, engineering, and differential equations.

Generalizations of convolution have applications in the field of numerical analysis and numerical linear algebra, and in the design and implementation of finite impulse response filters in signal processing.[citation needed]

Computing the inverse of the convolution operation is known as deconvolution.

 

https://en.wikipedia.org/wiki/Convolution

Convolution - Wikipedia

정의

두 개의 함수 f와 g가 있을 때, 두 함수의 합성곱을 수학 기호로는 f*g,와 같이 표시한다.

합성곱 연산은 두 함수 f, g 가운데 하나의 함수를 반전(reverse), 전이(shift)시킨 다음, 다른 하나의 함수와 곱한 결과를 적분하는 것을 의미한다. 이를 수학 기호로 표시하면 다음과 같다.

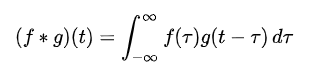
또한 g 함수 대신에 f 함수를 반전, 전이 시키는 경우 다음과 같이 표시할 수도 있다. 이 두 연산은 형태는 다르지만 같은 결과값을 갖는다.

 

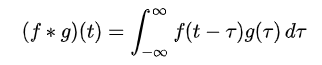
위의 적분에서 적분 구간은 함수 f와 g가 정의된 범위에 따라서 달라진다.

또한 두 확률 변수 X와 Y가 있을 때 각각의  확률 밀도 함수를 f와 g라고 하면, X+Y의 확률 밀도 함수는

f*g로 표시할 수 있다.

Convolution & Correlation

Convolution, 합성곱 

위키피디아에서 Convolution(영문)을 찾아보면 보면 정의는 다음과 같이 되어있습니다.

- 1D Convolution

- 2D Convolution

 Correlation, 상관분석

수식 정의는 다음과 같습니다.

- 1D Correlation

- 2D Correlation

Convolution과 Correlation수식을 잘 보면, 단지 +와 -에 대한 차이밖에 없습니다. 그리고 만약 입력함수가 y축에 대칭적이라면 Convolution의 정의에 따라 입력함수가 좌/우 반전이 되더라도 입력함수의 모양은 같기 때문에 Convolution과 Correlation은 같게 됩니다. 하지만 Convolution과 Correlation을 사용하는 용도와 의미는 서로 다릅니다.

 

Correlation

 입력함수(파란색)와 대상 함수 혹은 시스템 함수(빨간색)을 그대로 두고(좌/우 반전없이), 입력함수를 시간 축에 따라 움직이며(sliding), 대상 함수 혹은 시스템 함수와 겹치는 면적을 그래프로 나타냄을 알 수 있습니다.

 

 

선형시불변시스템(LTI)의 Convolution

  '입력 신호` 및 `시스템` 간의 상호관계를 명확히 표현   ☞ 임펄스 응답 참조
     - 선형 시불변 시스템(LTI)의 성질을 나타내는 등 중요한 수학적 수단이 됨

  LTI 시스템 응답 y(t)가,
     - 입력 x(t)와 임펄스응답 h(t)와의 합성곱 적분 형태의 컨볼루션으로 출력됨  
         

 

콘볼루션(Convolution), 상관성(Correlation) 비교

두 표현식이 비슷하나,
     - Convolution 은, 연산 작용 임
        . 원래의 변수가 출력에도 그대로 살아있는 연산의 일종임
        . 그 결과가, 자신이 속해있는 공간 그 자체로 보내지는 것을 말함
     - Correlation 은, 변환 작용 임
        . 원래의 변수가 다른 변수로 바뀌어 출력에 나타나는 변환의 일종임
        . 그 결과가, 자신이 속한 공간이 아닌, 타 공간에 보내지는 것을 말함
        . 변환 : 표현 영역을 바꾸어 달리 표현함으로써 해석 용이,취급 단순화 등을 도모


     - Convolution 은, 다른 용도를 위한 수학적 도구 역할이 강조된 연산
     - Correlation 은, 함수 간에 유사성의 비교 척도로 즉각 할용되는 변환

 

영상처리 관점에서의 Convolution

 

 아래 왼쪽과 같은 image에 가우시안 함수를 convolution하면 아래 오른쪽 그림과 같은 결과가 나옵니다. 이 방법은 영상처리를 해보신 분들은 다 아시는 가우시안 블러입니다.

 

실제 영상처리에서는 가우시안 블러를 Gaussian Kernel Filter를 사용하여 주변 pixel들의 가중치를 고려, 새로운 pixel을 할당하는 방법으로 사용합니다.

 

 

 

영상 신호: 512x512 해상도의 Lena 영상

임펄스 응답       : [0.2, 0.2, 0.2, 0.2, 0.2], 저대역 통과 필터

임펄스 응답       : [-1, 2, 1], 고대역 통과 필터

[Reference]

https://en.wikipedia.org/wiki/Convolution